

Determine the maximum height.įirst, find the vertical component of the initial velocity (v oy ) : An object projected upward at an angle θ = 30 o with the horizontal has an initial speed of 20 m/s. The initial velocity (v o ) = 12.5 √ 2 m/s ( upward direction, positive )Īcceleration due to gravity (g) = -10 m/s 2 ( downward direction, negative )Ĭalculated using the equation of the uniform linear motion with constant velocity.ĭ = v t = ( 12.5 √ 2 )( 2.5 √ 2 ) = ( 12.5 )( 2.5 )(2) = 62.5 meter sĥ. The time in air calculated with the equation of the upward vertical motion.Ĭhoose upward direction as positive and downward direction as negative. The x motion occurs at constant velocity and the y motion occurs at constant acceleration of gravity. Projectile motion could be understood by analyzing the horizontal and vertical component of the motion separately. The vertical component of the initial velocity : The horizontal component of the initial velocity : A kicked football leaves the ground at an angle θ = 45 o with the horizontal has an initial speed of 25 m/s. Acceleration due to gravity = 10 m/ s2, what is the time interval before the object hits the ground.Īcceleration due to gravity (g) = 10 m/s 2Ĥ. At the height of 2 km, an object is dropped from the aircraft. An aircraft is moving horizontally with a speed of 50 m/s. What is the time interval the object in air.ģ. The height of the object is the same when the time interval = 1 second and 3 seconds. G = acceleration due to gravity = 10 m/s 2Ģ. V oy = the initial velocity at the horizontal direction = 10√3 m/s V ty = the final velocity in the vertical direction = the final velocity at the highest point = 0 m/s The time interval to reach the maximum height, calculated using this equation : The initial velocity at the vertical direction (y axis) : The initial velocity at the horizontal direction (x axis) : Wanted : The time interval to reach the maximum height The initial velocity of bullet (v o) = 20 m/sĪcceleration due to gravity (g) = 10 m s –2 What is the time interval to reach the maximum height? A bullet fired a t an angle θ = 60 o with a velocity of 20 m/s. The most useful equation for this is usually y = viy t +0.5ay*t2. Finally, the peak height of the projectile can be found using a time value that is one-half the total time of flight. With the time determined, use a horizontal equation (usually x = vix t + 0.5ax*t2 ) to determine the horizontal displacement of the projectile. For non-horizontally launched projectiles, the second equation listed among the vertical equations (vfy = viy + ay*t) is usually the most useful equation. Select either a horizontal or vertical equation to solve for the time of flight of the projectile. Identify the unknown quantity that the problem requests you to solve for. For convenience sake, make a table with horizontal information on one side and vertical information on the other side. Carefully read the problem and list known and unknown information in terms of the symbols of the kinematic equations.
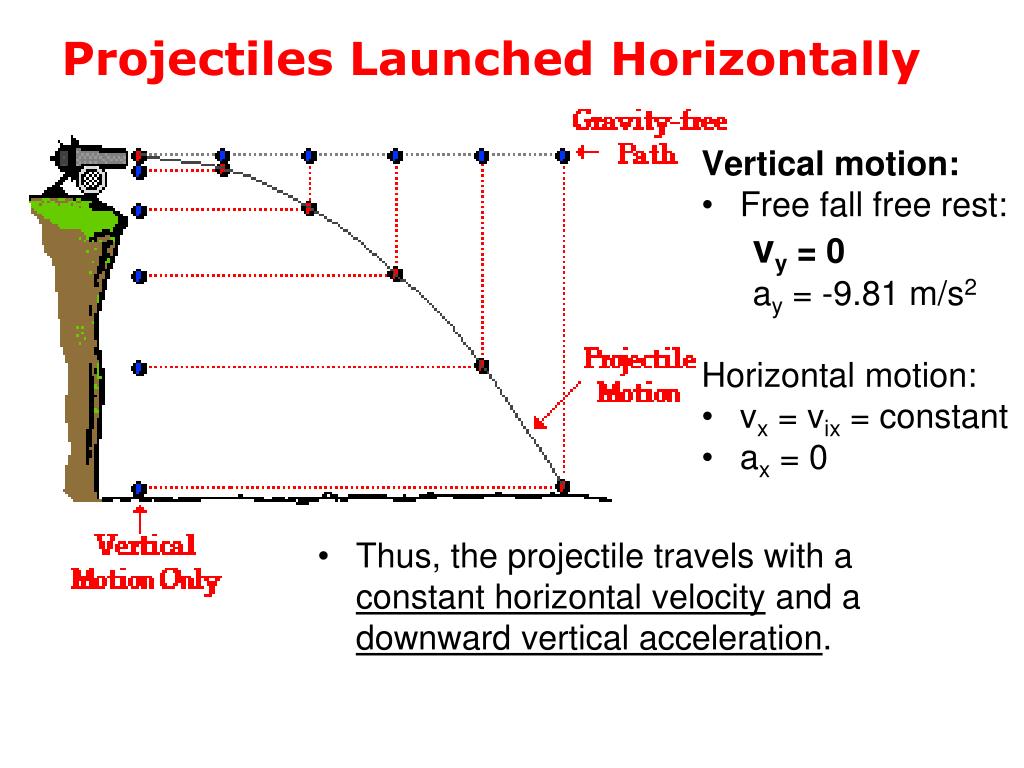
Use the given values of the initial velocity (the magnitude and the angle) to determine the horizontal and vertical components of the velocity (vix and viy).


 0 kommentar(er)
0 kommentar(er)
